 technology
download
papers
about
contact
technology
download
papers
about
contact
Audio compression algorithms typically use some form of transform coding where the time-domain audio signal is transformed to the frequency domain before quantisation, entropy coding and frame packing to a bitstream (Fig. 1). A psychoacoustic model determines a target noise shaping profile, which is used to allocate bits to transform coefficients such that quantisation errors are least audible to the human ear. In a conventional fixed-bitrate encoder the bit allocation is typically achieved with a recursive algorithm that attempts to meet the noise-shaping requirement within a bitrate constraint [1]. It is the bit allocation and quantisation stages of the coding process that are most affected by scalability issues - the time-frequency transform and psychoacoustic model in a scalable coder can be similar to a fixed-rate design.
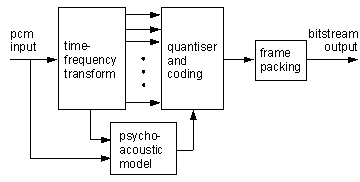
Fig. 1. Perceptual transform encoder for audio compression.
A simple approach to achieving scalability is the ‘error-feedforward’ arrangement where a core coder produces the lowest ‘embedded’ bit rate, and subsequent layers progressively reduce the error due to the core [2]. However, a significant amount of side information is associated with each layer which can reduce coding efficiency, and the number of possible decoding rates is limited to the number of layers.
An alternative approach to achieving scalability is ordered bitplane coding of transform coefficients, where in each frame coefficients are arranged in sign-magnitude format and magnitude bits are coded in order of significance, beginning with the most significant bits (MSB's) and progressing to the LSBs. This results in fully embedded coding where the bitstream at a certain rate contains all lower-rate codes, allowing low-complexity bitrate scaling by simply truncating coded frames. A related advantage is that variable-bitrate coding can be easily implemented by truncating each coded frame at an appropriate point before packing the bitstream. Bitplane coding exhibits fine-grain scalability in contrast to the coarse granularity offered by error-feedforward systems, and generates an ordered bitstream syntax which can simplify source-coding efforts to improve error resilience. In addition to these benefits, bitplane coding can also yield a significant increase in encoding speed since quantisation typically requires a single scan through the transform coefficients of each frame, as opposed to the recursive bit allocation search executed in fixed-rate coding.
Ordered bitplane coding is the basis of zero-tree quantisation used in image coding [3], [4], and can also be used for scalable audio coding. For example, Bit-Sliced Arithmetic Coding (BSAC) described by Park and co-workers [5] uses arithmetic coding of bitplane data, and bitplane coding is also used in Microsoft's Embedded Audio Coder (EAC).
Scala's encoder design follows the generic structure outlined in Fig. 1, where a modified discrete cosine transform (MDCT) is used to transform input samples to the frequency domain before quantisation and coding. Scala's scalable quantisation algorithm is based on bitplane runlength coding, using simple adaptive runlength codes to achieve high coding efficiency and low computational complexity without the use of Huffman or arithmetic coding. A custom psychoacoustic model and significant weight coding are used to spectrally shape quantisation errors so as to be minimally audible, while maintaining high coding efficiency at lower bitrates.
WINSAC, a Windows application that can decode scalable bitstreams generated with Scala's encoding algorithm, is available from the download area of this site.
A useful theoretical measure of coding efficiency is to record the average proportion of total bitrate allocated to coding significant (non-zero) transform coefficients in each frame, a metric that is closely related to Johnston’s description of perceptual entropy [6]. Fig. 2 compares the perceptual entropy coding efficiency of the Scala quantisation algorithm with two reference coders across a range of bitrates. At each bitrate efficiency is averaged across 3 challenging single-channel test pieces (harpsichord, pitchpipe, and female voice), each coded with full (22 kHz) bandwidth.
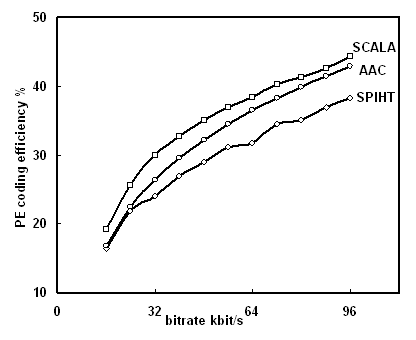
Fig. 2. Perceptual entropy efficiency as a function of bitrate.
The reference quantisation algorithms used to generate the data shown in Fig. 2 use the same transform and psychoacoustic model as the Scala algorithm, and correspond to:
AAC - these results simulate the behaviour of the fixed-bitrate multi-dimensional Huffman coding algorithm used in the MPEG-2/4 AAC coder [7], where the average bitrate requirement for each frame can be shown to closely approximate the 1-dimensional entropy of quantised coefficient values [8];
SPIHT - Said and Pearlman's bitplane coding algorithm [4], adapted for use with one-dimensional transform arrays typical with audio coding [9].
Fig. 2 indicates the coding efficiency of the Scala coder comfortably exceeds the scalable SPIHT algorithm, and also exceeds the performance of the fixed-rate AAC reference coder. Averaged across the bitrate range 32 - 96 kbit/s, the theoretical bitrate advantage for the Scala quantisation algorithm relative to AAC is approximately 4 %.
The Scala coding algorithm achieves quantisation in the encoder within a single pass of transform coefficients, in contrast to the iterative bit allocation approach typically used in fixed-bitrate coders such as MPEG-AAC. Consequently the Scala codec exhibits a significant reduction in computational load, a benefit reflected in increased encoding speed.
The current version of the Scala codec does not use inter-frame prediction, temporal noise shaping (TNS), variable-bitrate coding or intensity stereo. Most of the computational requirement in the encoder is due to the psychoacoustic model. Because psychoacoustic model calculations are confined to the encoder, decoder complexity is low.
While in principle the bitplane coding algorithm used in the Scala codec allows coded frames to be truncated at any point with a bitrate granularity of 1 bit/frame, the bitstream syntax currently used restricts bitrate granularity to 16-bit atoms. At typical sample rates this results in bitrate granularity of 0.7 kbit/s.
Scala's coding algorithm does not use inter-frame prediction, and each frame of data received by the decoder can be decoded independently without any knowledge of previous frames. Source coding techniques including error-resilient significant weight coding are used to produce bitstreams that are robust against transmission errors, so that corrupted frames remain decodeable and will not cause decoder crashes. Channel coding techniques such as error correction are not used.
Error resilience is achieved with only a small reduction in coding efficiency relative to the standard (unprotected) codec. A simple error concealment strategy ensures graceful degradation of coding quality in the event of transmission errors.
The MDCT transform used in the Scala codec is similar to the block-switched transform used in MPEG-AAC, with a frame length of 1024 samples. Combined encoder-decoder delay is approximately 1600 samples including lookahead, equivalent to 36 ms at typical sample rates.
[1] J. D. Johnston, "Transform Coding of Audio Signals Using Perceptual Noise Criteria," IEEE J. Select Areas in Communications, vol. 6, pp. 314 - 323 (1988 Feb.).
[2] J. Herre et al., "The Integrated Filterbank Based Scalable MPEG-4 Audio Coder," presented at the 105th Convention of the Audio Engineering Society, San Francisco, paper 4810 (1998).
[3] J. M. Shapiro, "Embedded Image Coding Using Zerotrees of Wavelet Coefficients," IEEE Trans. Sig. Proc., vol. 41, pp. 3445 - 3462 (1993 Dec.).
[4] A. Said and W. A. Pearlman, "A New, Fast, and Efficient Image Codec Based on Set Partitioning in Hierarchical Trees," IEEE Trans. Circuits and Sys. Video Tech., vol. 6, pp. 243-250 (1996 June).
[5] S. H. Park et al., "Multi-Layer Bit-Sliced Bit Rate Scalable Audio Coding," presented at the 103rd Convention of the Audio Engineering Society, New York, paper 4520 (1997 Sep.).
[6] J. D. Johnston, "Estimation of Perceptual Entropy Using Noise Masking Criteria," Proc. ICASSP 1988, pp. 2524 - 2527 (1988).
[7] M. Bosi et al., "ISO/IEC MPEG-2 Advanced Audio Coding," J. Audio Eng. Soc., vol. 45, pp. 789 - 812 (1997 Oct.).
[8] M. A. Watson and M. Truman, "Analyzing the Performance of Lossless Coding Techniques Used in Audio Coders," presented at the 109th Convention of the Audio Engineering Society, Los Angeles, paper 5275 (2000 Sep.).
[9] C. Dunn, "Efficient Audio Coding with Fine-Grain Scalability", presented at the 111th Convention of the Audio Engineering Society, New York, paper 5492 (2001 Nov.).
A detailed discussion of this work is contained within the following papers:
C. Dunn, "Scalable Bitplane Runlength Coding", presented at the 120th Convention of the Audio Engineering Society, Paris, paper 6749 (2006 May).
C. Dunn, "Aspects of Scalable Audio Coding", presented at the 122nd Convention of the Audio Engineering Society, Vienna, paper 7081 (2007 May).